Moosh is a code running under Octave/Matlab/Scilab, that allows to quickly simulate the propagation of a light beam in a multilayered structure. It has been optimized and it is very stable.
It will allow you to illustrate a lot of physical situations, ranging from the simplest refraction to the reflection by a Bragg mirror, as illustrated by the fly below.
Antoine Moreau
This numerical swiss army knife will allow you, whatever the multilayered structure you are considering, to get the reflection coefficient as a function of angle or wavelength, and to generate a corresponding image of the propagation of a beam inside the structure. This code will run with Octave, Matlab or Scilab, three platforms that are extremely close to each other. Octave and Scilab are freely available on any platform (Linux, Apple, Windows).
Source code used to get the figure.
Source code used to get the figure.
Source code used to get the figure.
Source code used to get the figure.
Source code used to get the figure.
Source code used to get the figure.
Source code used to get the figure.
Source code used to get the figure.
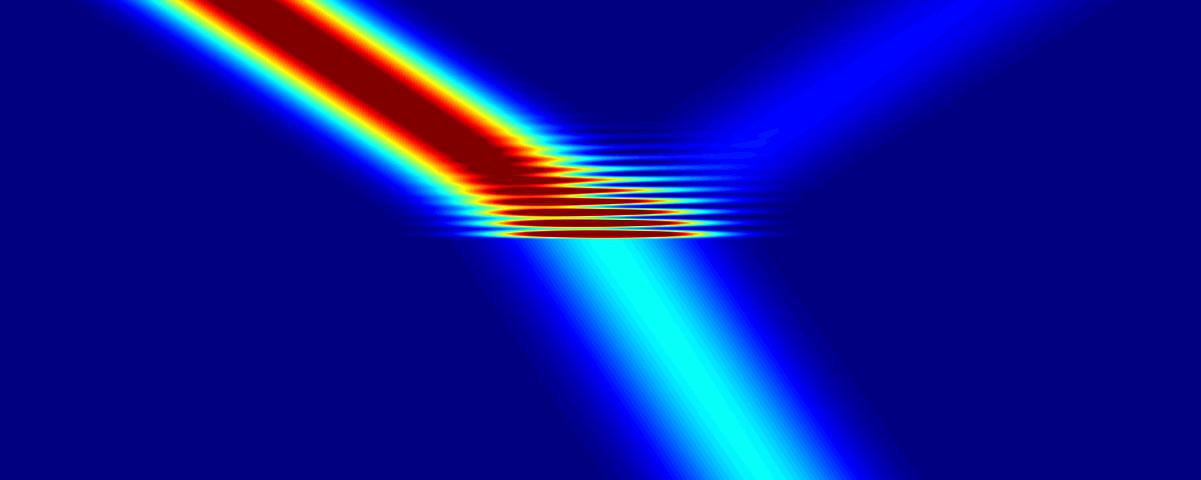
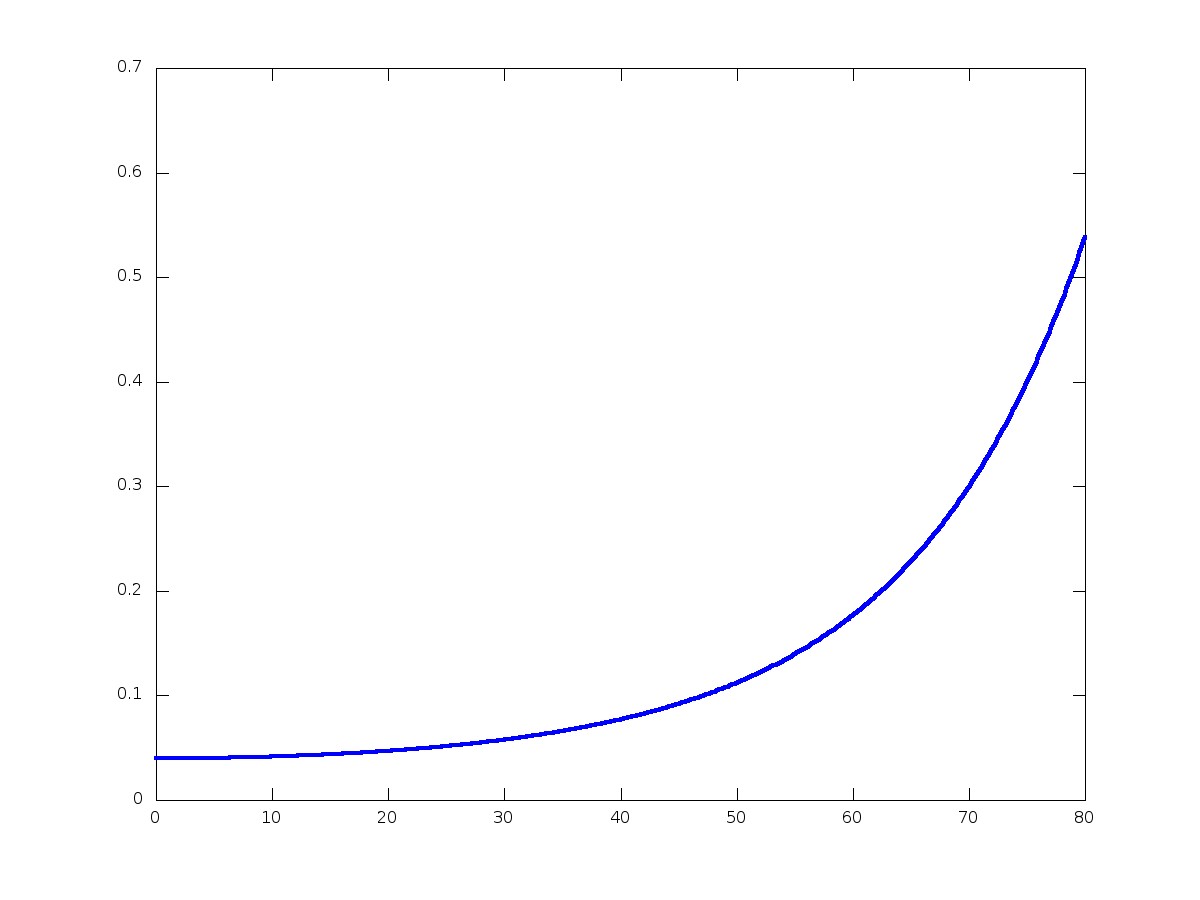
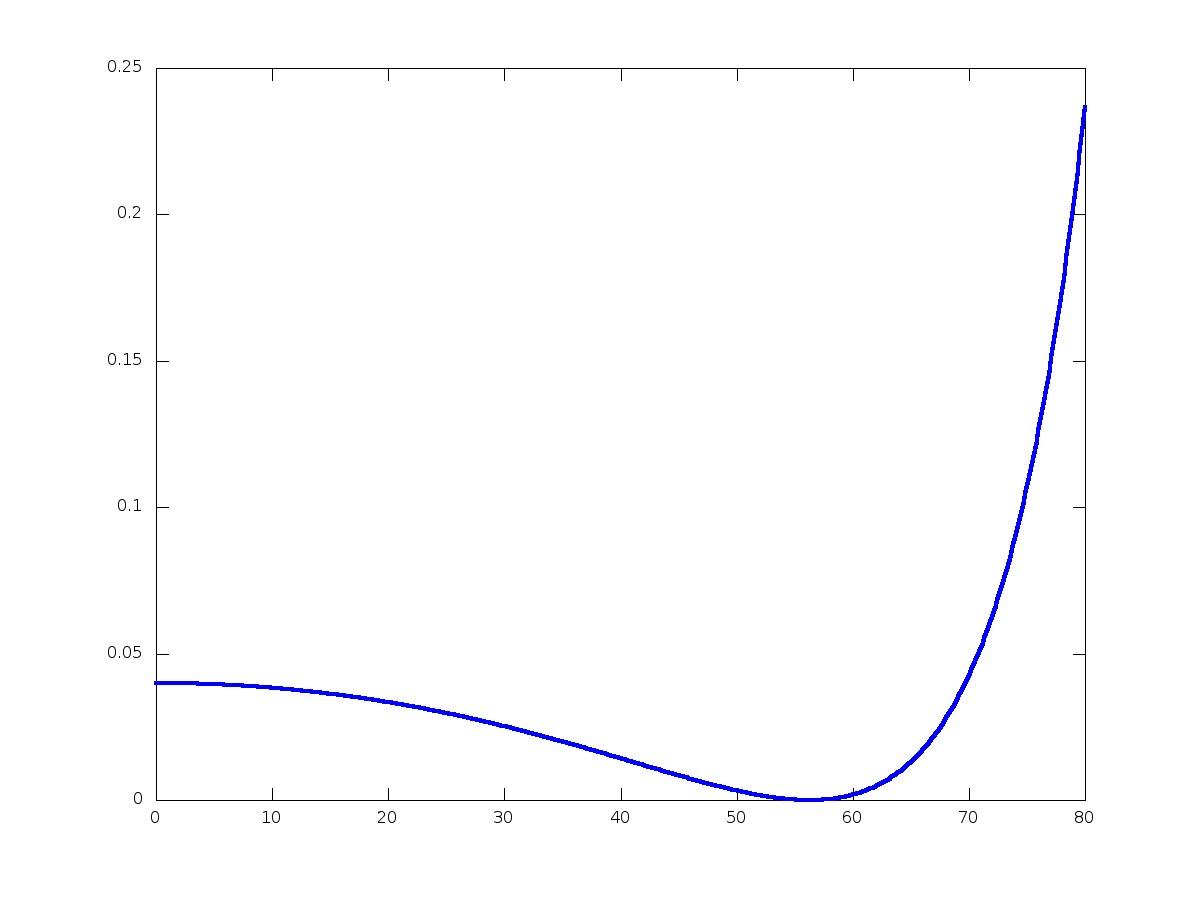
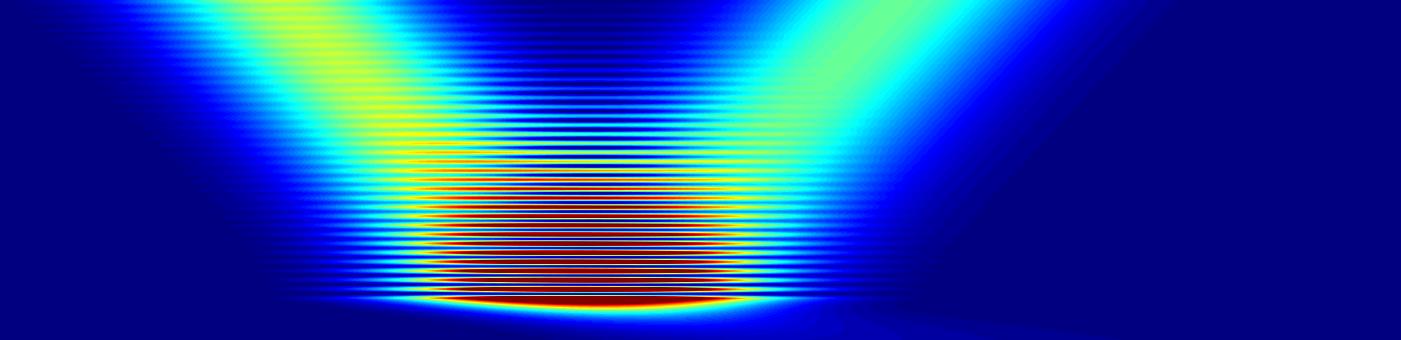
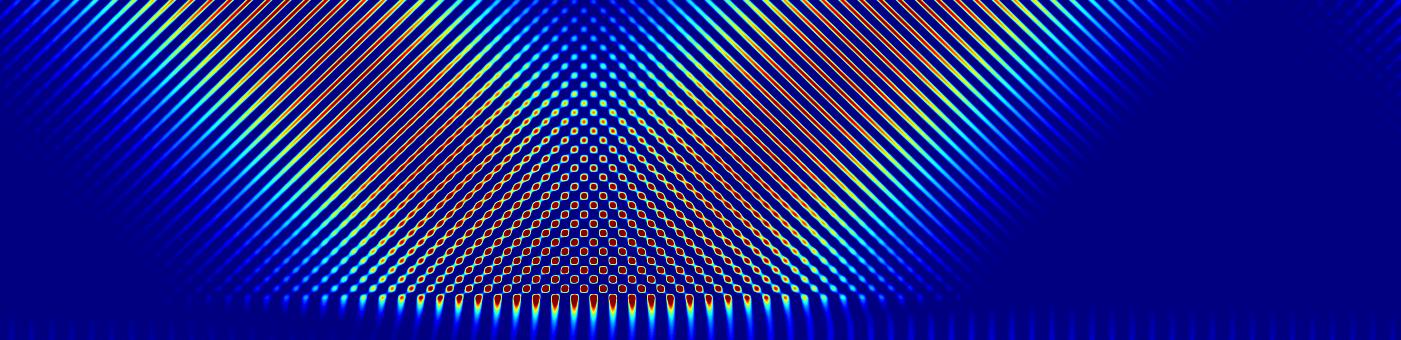
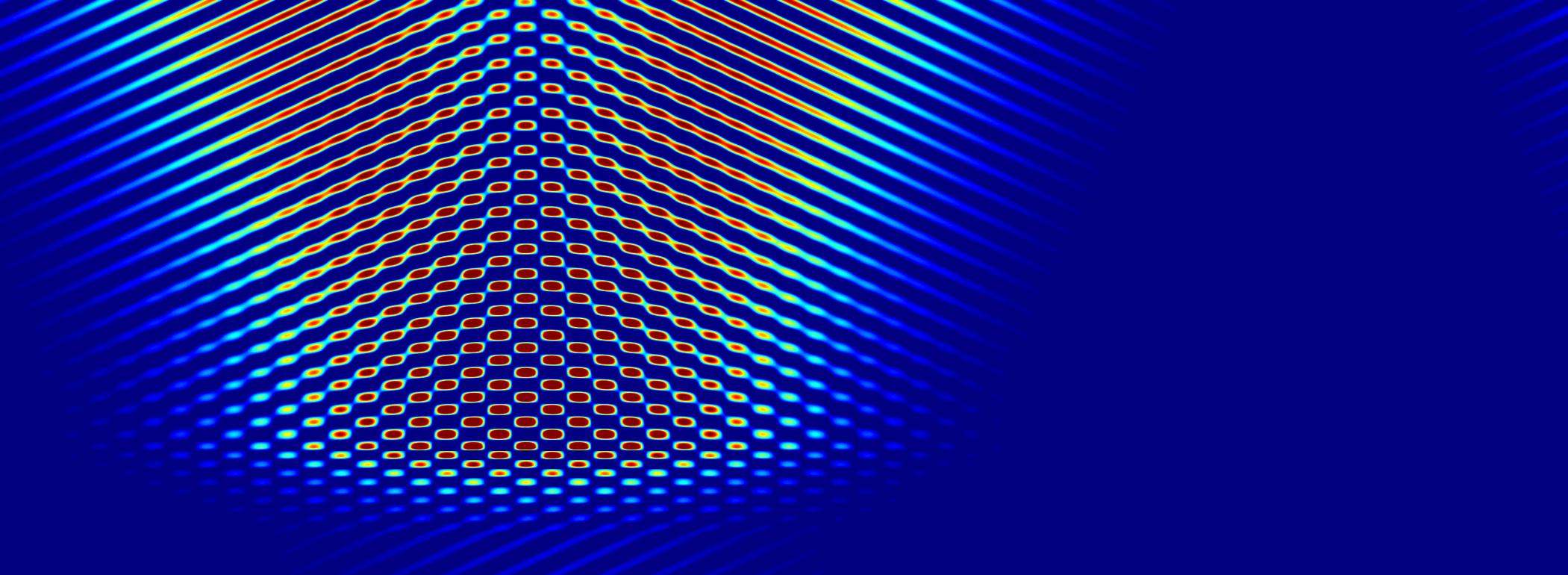
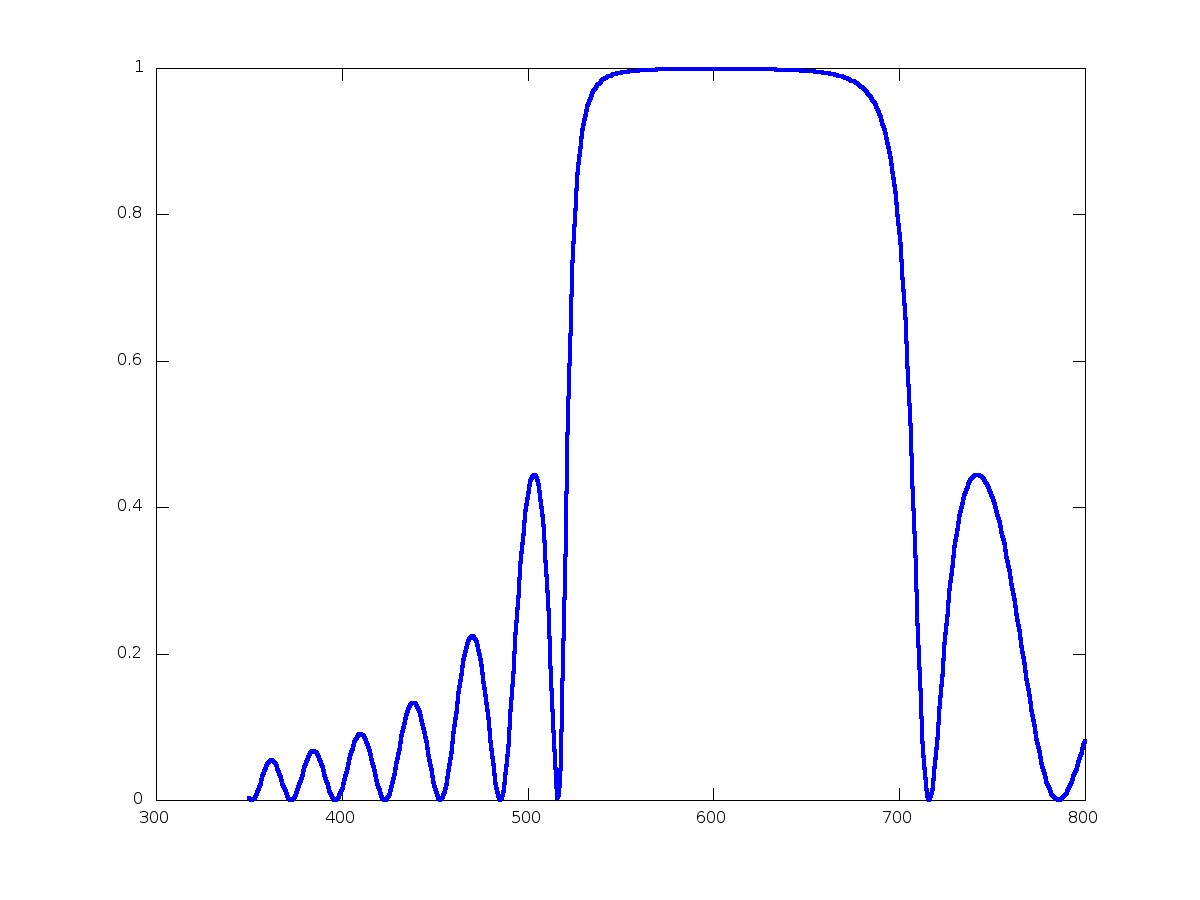
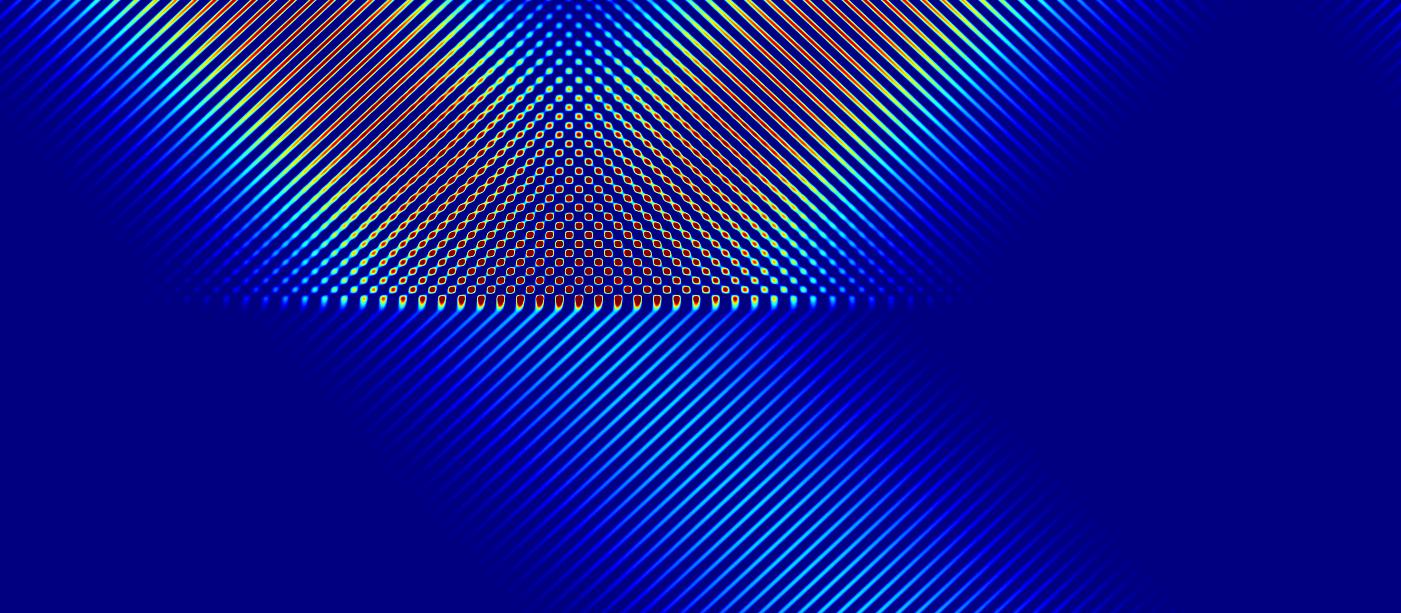
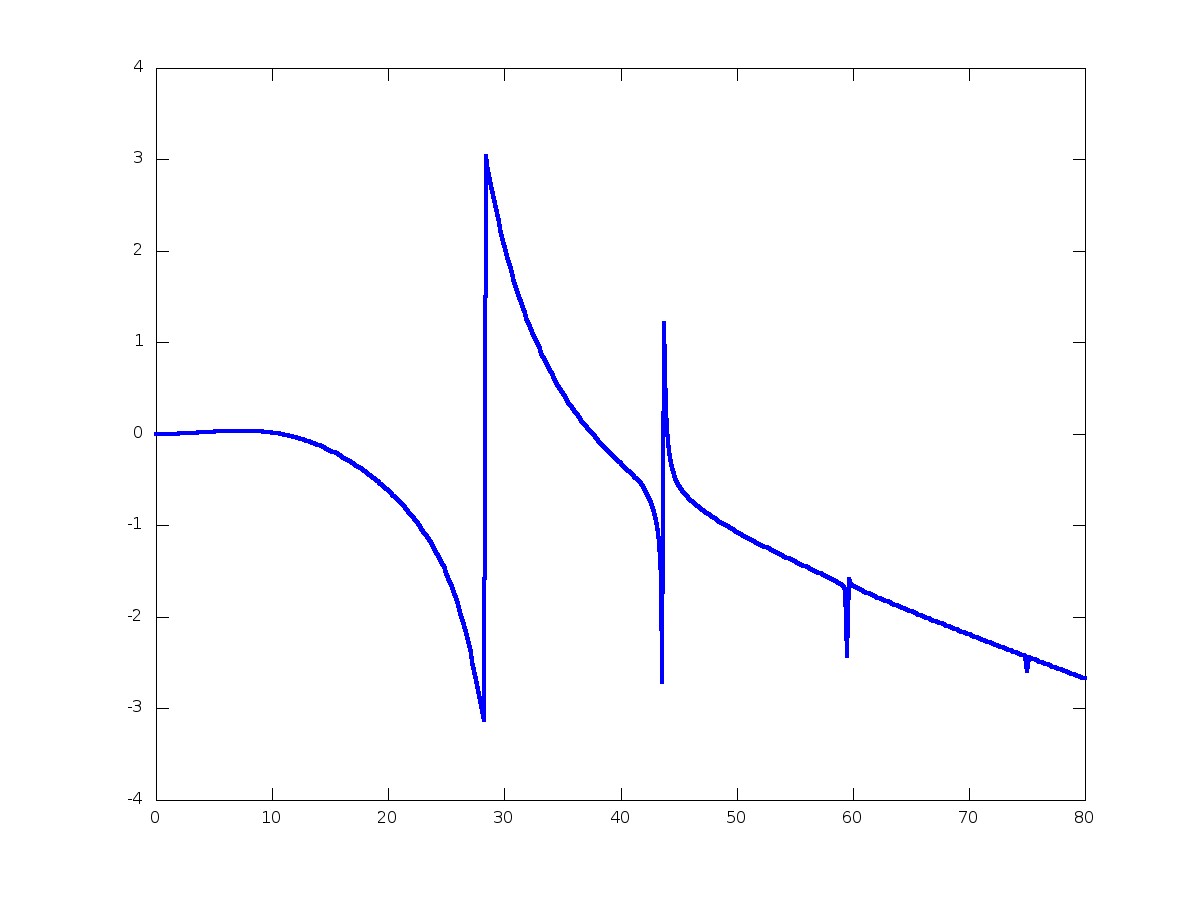
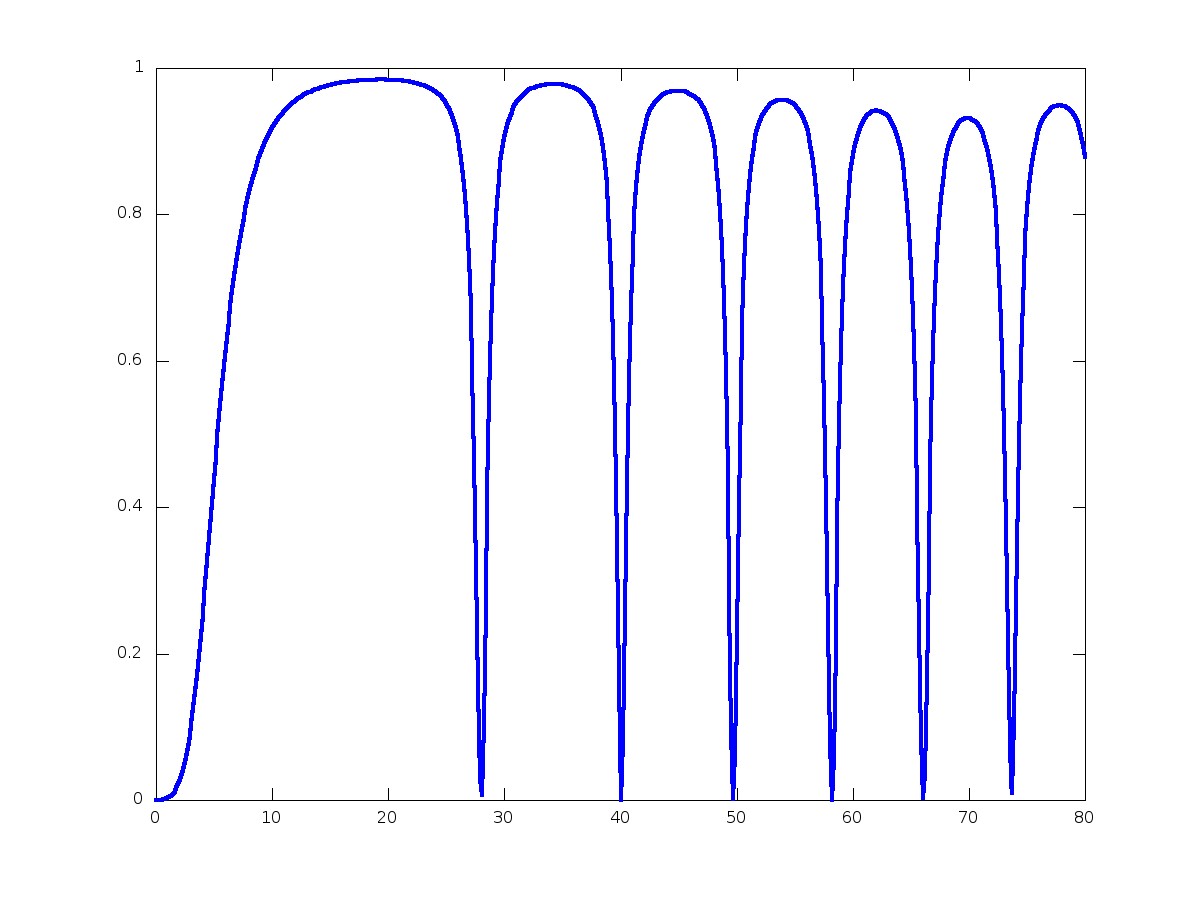When changing the angle, new resonances appear.
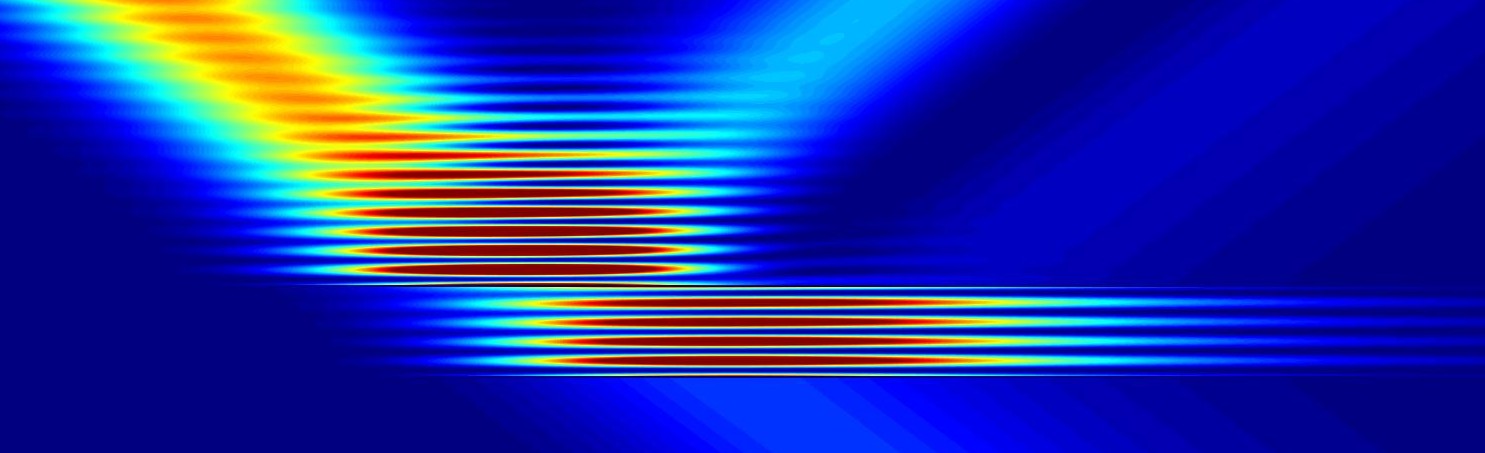The resonances are in this case analogous to guided modes.
Source code used to get the figure.
Source code used to get the figure.
Source code used to get the figure.
Source code used to get the figure.
Source code used to get the figure.
